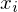On Mon, Mar 23, 2020 at 6:08 AM Nicklas Karlsson <
address@hidden> wrote:
Then thinking again. Sometimes point will end up outside the area in between the three nearest neighbours. Or maybe more correctly expressed in mathematical terms, point sometimes end up outside the convex hull spent up by the three nearest neighbours.
Maybe the weighted estimator will work, have to think. Whole data set will most probably work well, there are only about 100 points and guess plot figure use more exuction time. Averaging over points piled up is the correct solution.
For some reason Octave delaunay(...) function return a screwed up mesh, some angles are very small while others are very wide. This might be because most of the points are rather squared with a small scew while in one corner points in the outer corner is squeezed to a line because of limited signal. Then mesh is screwed up interpolation does not work well.
Matlab has a 'scatteredInterpolant' function that is still in the wish list for Octave. But Octave does have griddata. you give the function your scattered data points as three vectors x, y, f(x,y), and request output points (or grid) xi, yi, and it will apply one of the methods it has implemented. Currently only
'nearest neighbor' interpolation and linear interpolation are implemented in the octave releases. I just implemented the Biharmonic spline interpolation (smooth interpolant, the 'v4' option in matlab) in bug #33539 but haven't worked up a full patch yet. Also looking for proper matlab compatible cubic and 'natural' method interpolations.
linear, cubic, and natural methods are all triangulation based. they take the scattered points, use octave's delauney triangulation, then calculate local interpolants within the triangles. linear (actually bilinear i guess) is simply a weighted some of triangle areas (the interpolation point creates three sub-triangles within the mesh triangle, and value is a weighted projection inversely proportional to sub-triangle size, where a big sub-triangle has you more strongly weighted toward the point not associated with that sub-triangle). the v4 method does not triangulate, and does a weighted interpolation over the entire mesh. that can get slow and memory intensive, but it's currently the only 'smooth' interpolation function Octave has implemented (sort of).
it sounds like griddata should do what you want, unless I've misread the thread.