If you're trying to use mesh techniques, I guess you will prefer this solution : it's computationally less demanding, and it makes the interpolant function smooth.
In this case, when the density is high, and points "pile up", then the estimated
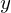 will be
averaged over those points : it's up to you to decide whether this
corresponds to your model or not.
will be
averaged over those points : it's up to you to decide whether this
corresponds to your model or not.In the formula above, you can restrict
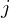 to to the
3 nearest neighbours, or use the whole data set if you can afford
the computational load.
to to the
3 nearest neighbours, or use the whole data set if you can afford
the computational load.For the radial basis function, you can use for instance a gaussian kernel :
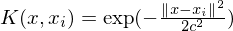
if
 is low,
the interpolant will be "blurry", if
is low,
the interpolant will be "blurry", if  is high it
will be "spiky".
is high it
will be "spiky".On 12/03/2020 15:53, Nicklas Karlsson wrote:
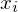 means the
means the 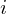 -th point in
your data, so x(i,:) or x(:,i) in your code)
-th point in
your data, so x(i,:) or x(:,i) in your code)