Then thinking again. Sometimes point will end up outside the area in between the three nearest neighbours. Or maybe more correctly expressed in mathematical terms, point sometimes end up outside the convex hull spent up by the three nearest neighbours.
Maybe the weighted estimator will work, have to think. Whole data set will most probably work well, there are only about 100 points and guess plot figure use more exuction time. Averaging over points piled up is the correct solution.
For some reason Octave delaunay(...) function return a screwed up mesh, some angles are very small while others are very wide. This might be because most of the points are rather squared with a small scew while in one corner points in the outer corner is squeezed to a line because of limited signal. Then mesh is screwed up interpolation does not work well.
Thanks, Nicklas Karlsson
Den mån 16 mars 2020 kl 10:02 skrev Augustin Lefèvre <address@hidden>:
You can use 3-nearest neighbour interpolation :
y=13∑j=13yjy = \frac{1}{3} \sum_{j=1}^3 y_j
where j is the index of the three nearest neighbours (based on xx values)
or a weighted estimator :
y=∑j=1nK(x,xj)yj∑j=1nK(x,xj)y = \frac{\sum_{j=1}^n K(x,x_j) y_j}{\sum_{j=1}^n K(x,x_j)}
(careful,means the
-th point in your data, so x(i,:) or x(:,i) in your code)
If you're trying to use mesh techniques, I guess you will prefer this solution : it's computationally less demanding, and it makes the interpolant function smooth.
In this case, when the density is high, and points "pile up", then the estimatedwill be averaged over those points : it's up to you to decide whether this corresponds to your model or not.
In the formula above, you can restrictto to the 3 nearest neighbours, or use the whole data set if you can afford the computational load.
For the radial basis function, you can use for instance a gaussian kernel :
ifis low, the interpolant will be "blurry", if
is high it will be "spiky".
On 12/03/2020 15:53, Nicklas Karlsson wrote:
I have some problem with interpolation on scattered data. griddata(...) or interp2(...) functions do not work well. Delaunay function could triangulate data but maybe not well in all cases.
I have function to find nearest points. Interpolate between the three nearest point should if I think correct be equal to interpolation on delaunay triangulation but me a little bit stupid and can't immidiately figure out the equation. Anyone have it at hand?
I however found two other very interesting functions here http://fourier.eng.hmc.edu/e176/lectures/ch7/node7.html called "Radial Basis Function Method" and "Shepard method". I am however a little bit uncertain what happen then density vary for example then many points are tightly spaced as I expect them to pile up. Anyone used any of these?
Regards Nicklas Karlsson
 means the
means the 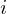 -th point in
your data, so x(i,:) or x(:,i) in your code)
-th point in
your data, so x(i,:) or x(:,i) in your code)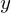 will be
averaged over those points : it's up to you to decide whether this
corresponds to your model or not.
will be
averaged over those points : it's up to you to decide whether this
corresponds to your model or not.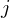 to to the
3 nearest neighbours, or use the whole data set if you can afford
the computational load.
to to the
3 nearest neighbours, or use the whole data set if you can afford
the computational load.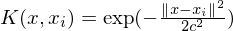
 is low,
the interpolant will be "blurry", if
is low,
the interpolant will be "blurry", if